Mean Flow Explained with High School Math
TL;DR: This blog explains the high-level ideas of mean flow with different levels of math.
1. High School Math
Let first solve a high-school math problem:
- An object moves along a straight line (so that speed = velocity), and we are interested in its average velocity $u(t)$ over the time interval $[0, t]$. We know that during the time interval $[3,3.1]$, the object’s velocity is constant 4.1 (units per second). It is also known that the average velocity at time $t=3.1$ is $0.1$ greater than the average velocity at time $t=3$. Find the average velocity at time $t=3$.
Solution:
\[\underbrace{3.1\left[u(3) + 0.1\right]}_{\text{distance traveled from t=0 to t = 3.1}} = \underbrace{3 u(3)}_{\text{distance traveled from t=0 to t = 3}} + \underbrace{0.1v(3)}_{\text{distance traveled from t=3 to t = 3.1}},\]where $v(3) = 4.1$. Solving this equation gives $u(3) = 1$.
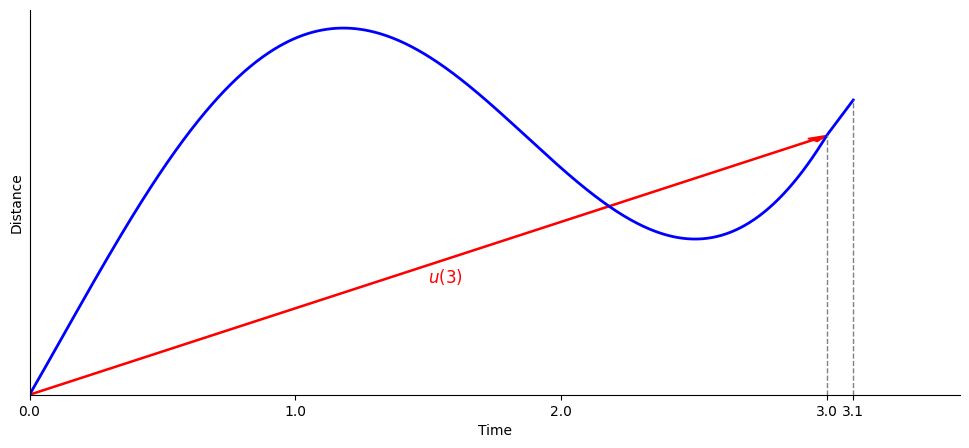
Takeaways:
- Given the instantaneous velocity $v(t)$ and how the average velocity changes, we can determine the average velocity.
- We have established a connection between the average velocity and the pair (instantaneous velocity, how the average velocity changes).
2. Calculus I
For the same problem above, instead of using actual numbers (e.g., $0.1,4.1,3,3.1$ ), we now express it symbolically and let the starting time be $r$ instead of 0. Thus, we are interested in $u(r, t)$, the average velocity from $t=r$ to $t=t$:
\[\underbrace{(t + \Delta t - r)}_{\text{time interval } [r, t+\Delta t]} \cdot \underbrace{\left(u(r, t) + \Delta u \right)}_{\text{average velocity over } [r, t+\Delta t]} = (t-r) u(t) + \Delta t v(t) .\]Simplify and isolate $u(t,r)$:
\[u(r, t) = v(t) - (t-r)\frac{\Delta u}{\Delta t} - \Delta u.\]Taking $\Delta t$ to be infinitesimally small: \(u(r, t) = v(t) - (t-r)\frac{d u(r,t)}{d t} .\)
Takeaway:
- Given the instantaneous velocity $v(t)$ and the rate of change of the average velocity $\frac{d u(r, t)}{d t}$, we can determine the average velocity $u(r, t)$.
3. A More Analytical Proof with Calculus I
Let $x(t)$ be the position of the object at time $t$, then by definition, $v(t)=\frac{d x}{d t}$ and
\[u(r, t)=\frac{x(t)-x\left(r\right)}{t-r}.\]Treating $r$ as a constant and differentiate both sides:
\(\frac{du(r, t)}{dt}=\frac{d}{dt}\left(\frac{x(t)-x\left(r\right)}{t-r}\right).\) By quotient rule rule on the R.H.S.:
\[\frac{du(r, t)}{dt}=\frac{(t-r) \frac{d x(t)}{d t}-[x(t)-x(r)]}{(t-r)^2}.\]Simplify by substituting $v(t)=\frac{d x}{d t}$ and $x(t)-x(r)=(t-r) u(r, t)$:
\[\frac{d u(r,t)}{d t}=\frac{(t-r) v(t)-(t-r) u(r,t)}{(t-r)^2}=\frac{v(t)-u(r,t)}{t-r} .\]Isolate $u(r,t)$: \(u(r, t)=v(t)-(t-r) \frac{d u(r,t)}{d t} .\)
4. Calculus III: The Mean Flow Math
Note that in flow matching, there isn’t just one trajectory. The velocities also depend on the space variable $X_t$. By definition, the instantaneous velocity $v(X_t, t) = \frac{dX_t}{dt}$ and the average velocity $u\left(X_t, r, t\right)$ over an interval $[r, t]$ with $t > r$ is defined as:
\[u(X_t, r, t) \triangleq \frac{1}{t - r} \int_{r}^{t} v(X_s, s) ds.\]Moving terms and differentiating both sides:
\[\frac{d}{dt}\!\big[(t - r)\, u(X_t, r, t)\big] = \frac{d}{dt} \int_{r}^{t} v(X_s, s)\, ds.\]By chain rule on the left and the Fundamental Theorem of Calculus on the right:
\[u(X_t, r, t) + (t-r) \frac{d}{dt} u(X_t, r, t)=v(X_t, t).\]Clearing up:
\[\underbrace{u(X_t, r, t)}_{\text{avg. vel.}}= \underbrace{v(X_t, t)}_{\text{instant. vel.}}-(t - r) \underbrace{\frac{d}{dt} u(X_t, r, t)}_{\text{time derivative}}.\]Takeaway:
- Given the instantaneous velocity $v(X_t, t)$ and the rate of change of the average velocity $\frac{d}{dt} u(X_t, r, t)$, we can determine the average velocity $u(X_t, r, t)$.
- We can parametrize $u$ using a neural network and train it to match the LHS. by the conditional instantaneous velocity $v(X_t, t \mid X_1, X_0)$. Note that the time derivative can be computed through Autograd.
- Note that this time derivative is implicit; Autograd can only directly compute explicit (partial) derivatives. You can convert it with a chain rule and compute it by Jacobian Vector Product (
torch.autograd.functional.jvp). See details at this blog.
- Note that this time derivative is implicit; Autograd can only directly compute explicit (partial) derivatives. You can convert it with a chain rule and compute it by Jacobian Vector Product (